Obnjective:
The Program is used to Rotate a matrix if consecutive Integers Both Clockwise and Anti-Clockwise. In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space.
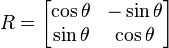 rotates points in the xy-Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv. Since matrix multiplication has no effect on the zero vector (i.e., on the coordinates of the origin), rotation matrices can only be used to describe rotations about the origin of the coordinate system.
Rotation matrices provide a simple algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. In 2-dimensional space, a rotation can be simply described by an angle θ of rotation, but it can be also represented by the 4 entries of a rotation matrix with 2 rows and 2 columns. In 3-dimensional space, every rotation can be interpreted as a rotation by a given angle about a single fixed axis of rotation (see Euler's rotation theorem), and hence it can be simply described by an angle and a vector with 3 entries. However, it can also be represented by the 9 entries of a rotation matrix with 3 rows and 3 columns. The notion of rotation is not commonly used in dimensions higher than 3; there is a notion of a rotational displacement, which can be represented by a matrix, but no associated single axis or angle.
rotates points in the xy-Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv. Since matrix multiplication has no effect on the zero vector (i.e., on the coordinates of the origin), rotation matrices can only be used to describe rotations about the origin of the coordinate system.
Rotation matrices provide a simple algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. In 2-dimensional space, a rotation can be simply described by an angle θ of rotation, but it can be also represented by the 4 entries of a rotation matrix with 2 rows and 2 columns. In 3-dimensional space, every rotation can be interpreted as a rotation by a given angle about a single fixed axis of rotation (see Euler's rotation theorem), and hence it can be simply described by an angle and a vector with 3 entries. However, it can also be represented by the 9 entries of a rotation matrix with 3 rows and 3 columns. The notion of rotation is not commonly used in dimensions higher than 3; there is a notion of a rotational displacement, which can be represented by a matrix, but no associated single axis or angle.
Screenshot:
Program Source Code:
The Program is used to Rotate a matrix if consecutive Integers Both Clockwise and Anti-Clockwise. In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space.
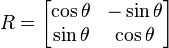 rotates points in the xy-Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv. Since matrix multiplication has no effect on the zero vector (i.e., on the coordinates of the origin), rotation matrices can only be used to describe rotations about the origin of the coordinate system.
rotates points in the xy-Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv. Since matrix multiplication has no effect on the zero vector (i.e., on the coordinates of the origin), rotation matrices can only be used to describe rotations about the origin of the coordinate system.
Rotation matrices are square matrices, with real entries. More specifically they can be characterized as orthogonal matrices with determinant 1:
 .
.
The set of all such matrices of size n forms a group, known as the special orthogonal group SO(n).
In two dimensions every rotation matrix has the following form:
 .
.
This rotates column vectors by means of the following matrix multiplication:
 .
.
So the coordinates (x',y') of the point (x,y) after rotation are:
 ,
, .
.
The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. -90°).
 .
.
Non-standard orientation of the coordinate system
If a standard right-handed Cartesian coordinate system is used, with the x axis to the right and the y axis up, the rotation R(θ) is counterclockwise. If a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics, which often have the origin in the top left corner and the y-axis down the screen or page.[1]
See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.
Common rotations
Particularly useful are the matrices for 90° and 180° rotations:
![R(90^\circ) = \begin{bmatrix}
0 & -1 \\[3pt]
1 & 0 \\
\end{bmatrix}](http://upload.wikimedia.org/wikipedia/en/math/d/b/c/dbcfcdc115372dfe6e66982a841f9076.png) (90° counterclockwise rotation)
(90° counterclockwise rotation)![R(180^\circ) = \begin{bmatrix}
-1 & 0 \\[3pt]
0 & -1 \\
\end{bmatrix}](http://upload.wikimedia.org/wikipedia/en/math/b/0/d/b0d7db5b1cf2e531126f13e1de38113b.png) (180° rotation in either direction – a half-turn)
(180° rotation in either direction – a half-turn)![R(270^\circ) = \begin{bmatrix}
0 & 1 \\[3pt]
-1 & 0 \\
\end{bmatrix}](http://upload.wikimedia.org/wikipedia/en/math/e/1/7/e17c4efcf457f9c618c5642111d8bb46.png) (270° counterclockwise rotation, the same as a 90° clockwise rotation)
(270° counterclockwise rotation, the same as a 90° clockwise rotation)
Screenshot:
Program Source Code:
/** * The Matrix Rotation Program rotates the Matrix Clockwise and Anti-Clockwise by 90 Degrees. * © SHANTANU KHAN * @ shantanukhan1995@gmail.com * @website 0code.blogspot.com * Program Type : BlueJ Program - Java */ import java.io.*; public class Matrix_Rotation { BufferedReader br=new BufferedReader(new InputStreamReader(System.in)); int row,col; int OriArr[][],NewArrAC[][],NewArrC[][]; void input()throws Exception { System.out.print("Enter the Size of the Row : "); row=Integer.parseInt(br.readLine()); System.out.print("Enter the Size of the Column : "); col=Integer.parseInt(br.readLine()); } void initialize() { OriArr=new int[row][col]; int n=1; for(int i=0;i<row;i++) { for(int j=0;j<col;j++) OriArr[i][j]=n++; } } void rotateClockwise() { NewArrC=new int[col][row]; int ro=0,co=0; for(int i=row-1;i>=0;i--) { for(int j=0;j<col;j++) NewArrC[j][i]=OriArr[ro][co++]; co=0; ro++; } } void rotateAntiClockwise() { NewArrAC=new int[col][row]; int ro=0,co=col-1; for(int i=0;i<col;i++) { for(int j=0;j<row;j++) NewArrAC[i][j]=OriArr[ro++][co]; ro=0; co--; } } void print() { System.out.println("Original Matrix :"); for(int i=0;i<row;i++) { for(int j=0;j<col;j++) System.out.print(OriArr[i][j]+" "); System.out.println(); } System.out.println("Clockwise Rotated Matrix :"); for(int i=0;i<col;i++) { for(int j=0;j<row;j++) System.out.print(NewArrC[i][j]+" "); System.out.println(); } System.out.println("Anti-Clockwise Rotated Matrix :"); for(int i=0;i<col;i++) { for(int j=0;j<row;j++) System.out.print(NewArrAC[i][j]+" "); System.out.println(); } } public static void main(String args[])throws Exception { Matrix_Rotation obj=new Matrix_Rotation(); obj.input(); obj.initialize(); obj.rotateClockwise(); obj.rotateAntiClockwise(); obj.print(); } }







0 comments :
Post a Comment